MEDIDAS DE DISPERSIÓN.
Las medidas de dispersión muestran la variabilidad de una distribución, indicándolo por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.
Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (desviación media) y otra es tomando las desviaciones al cuadrado (varianza).
DATOS INDIVIDUALES
Son el conjunto de observaciones que se presentan en su forma original tal y como fueron recolectados, para obtener información directamente de ellos.
Cuando en la muestra que se ha tomado de la población o proceso que se desea analizar se tienen menos de 30 datos, estos son analizados sin necesidad de formar clases con ellos y a esto es a lo que se le llama tratamiento de datos no agrupados.
Se emplea la ecuación:
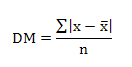
Ejemplo:
Calcular la desviación media de la distribución: 3, 8, 8, 8, 9, 9, 9, 18
Solución:
Se calcula la media aritmética.
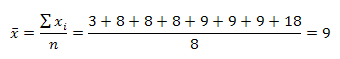
Se calcula la desviación media.
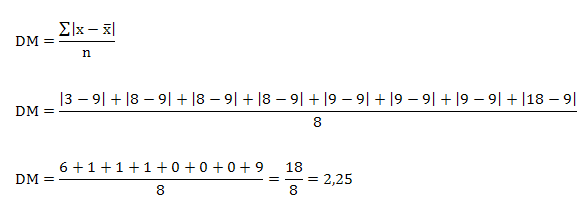
Varianza y desviación estándar
La varianza es la media aritmética de los cuadrados de las desviaciones respecto a la media aritmética, es decir, es el promedio de las desviaciones de la media elevadas al cuadrado. La desviación estándar o desviación típica es la raíz de la varianza.
La varianza y la desviación estándar proporcionan una medida sobre el punto hasta el cual se dispersan las observaciones alrededor de su media aritmética.
PROPIEDADES
- La varianza y desviación estándar (o cualquier otra medida de dispersión) indican el grado en que están dispersos los datos en una distribución. A mayor medida, mayor dispersión.
- La varianza es un número muy grande con respecto a las observaciones, por lo que con frecuencia se vuelve difícil para trabajar.
- Debido a que las desviaciones son elevadas al cuadrado y la varianza siempre se expresa en términos de los datos originales elevados al cuadrado, se obtiene unidades de medida de los datos que no tiene sentido o interpretación lógica. Por ejemplo, si se calcula la varianza de una distribución de datos medidos en metros, segundos, dólares, etc, se obtendrá una varianza mediada en metros cuadrados, segundos cuadrados, dólares cuadrados, respectivamente, unidades de medida que no tienen significado lógico respecto a los datos originales.
- Para solucionar las complicaciones que se tiene con la varianza, se halla la raíz cuadrada de la misma, es decir, se calcula la desviación estándar, la cual es un número pequeño expresado en unidades de los datos originales y que tiene un significado lógico respeto a los mismos.
A pesar de lo anterior, es difícil describir exactamente qué es lo que mide la desviación estándar. Sin embargo, hay un resultado útil, que lleva el nombre del matemático ruso Pafnuty Lvovich Chebyshev, y se aplica a todos los conjuntos de datos. Este teorema de Chebyshev establece que para todo conjunto de datos, por lo menos 1- 1/k2 de las observaciones están dentro de k desviaciones estándar de la media, en donde k es cualquier número mayor que 1. Este teorema se expresa de la siguiente manera:
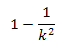
Así por ejemplo, si se forma una distribución de datos con k =3 desviaciones estándar por debajo de la media hasta 3 desviaciones estándar por encima de la media, entonces por lo menos
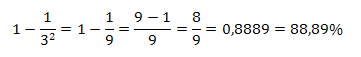
La varianza para una población se calcula con:

DATOS AGRUPADOS
Son aquellos datos que pertenecen a un tamaño demuestra mayor a 20 o más elementos, por lo que para ser analizados requieren ser agrupados en clases a partir de ciertas características. - Su objetivo es resumir la información. - Comúnmente, pertenecen a una muestra mayor a 20 elementos, por lo cual requieren ser agrupados, esto implica: ordenar, clasificar y expresar los en una tabla de frecuencias. - Se agrupan los datos, esto quiere decir que se pueden clasificar de forma coherente y lógica mediante una tabla de frecuencias. - La agrupación de los datos puede ser simple o mediante intervalos de clase.
Desviación media
La desviación respecto a la media es la diferencia entre cada valor de la variable estadística y la media aritmética.
Di = x - x
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 



Ejemplo
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:


Ejemplo
Calcular la desviación media de la distribución:
| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.174 | 21.428 |
| 21 | 457.5 | 98.57 |


Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por  .
.
 .
.
Varianza para datos agrupados

Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

Varianza para datos agrupados

Ejercicios de varianza
Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


TÉCNICAS DE CONTEO
Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.La enumeración de puntos muestrales en un espacio muestral, en ocasiones es difícil y laboriosa por la cantidad de puntos a contar o enumerar, propiciando quesee puedan cometer errores al emprender esa tarea. En estos casos se recurre al análisis combinatorio, que es una manera más sofisticada de contar.
DIAGRAMA DE ÁRBOL
Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades; consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final). Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar.

PRINCIPIO MULTIPLICATIVO
- Si una operación puede efectuarse de n maneras diferentes y realizada una cualquiera de ellas, una segunda operación puede efectuarse de p maneras distintas, entonces el número total (N) de maneras diferentes, en que pueden realizarse a la vez ambas operaciones es:N = n×p
- EJEMPLO: Si una persona ha de escoger como vestirse, teniendo 4 camisas, 6 pantalones, 5 pares de calcetines y 2 pares de zapatos, entonces tiene 4 × 6 × 5 ×2 = 240 formas de vestirse, ya que cada elección de la camisa (4 opciones) tiene 6 opciones para el pantalón, lo que da 4 × 6 = 24 opciones para la camisa y pantalón. Para cada una de esas 24 tiene 5 pares de calcetines, totalizando 120 formas, y para cada una de esas tiene dos opciones de los zapatos, de modo que se duplica el total y al final tiene 240 formas de vestirse. El principio de la multiplicación puede visualizarse mediante un diagrama de árbol.
PRINCIPIO ADITIVO
- Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ….. y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de, M + N +………+ W maneras o formas
- EJEMPLO: Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirlpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que
- Solución:M: Maneras de seleccionar una lavadora WhirlpoolN: Maneras de seleccionar una lavadora EasyW: Maneras de seleccionar una lavadora General Electric M = 2 x 4 x 2 = 16 maneras N = 3 x 2 x 2 = 12 maneras W = 1 x 2 x 1 = 2 maneras M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora.
PERMUTACIONES
Son eventos de tipo multiplicativo, donde el número de posibilidades va disminuyendo y si importa el orden una permutación es un arreglo de un conjunto de objetos en un orden definido. El número de permutaciones diferentes de estos objetos es ; esto se vé fácilmente si pensamos que para la primera alternativa disponemos de los elementos del conjunto, cada uno de los cuales puede complementarse con los restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto .
El número de permutaciones posibles al tomar objetos del conjunto de elementos será, siguiendo el mismo razonamiento.
PERMUTACIONES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ
Ejemplo : ¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?
Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:
8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320
PERMUTACIONES CIRCULARES
Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar al rededor de una mesa circular, ¿de cuántas formas lo podemos hacer?
Observemos los siguientes arreglos:

PERMUTACIONES SIN REPETICIÓN
Ejemplo 7: ¿ De cuántas formas diferentes se pueden sentar seis alumnos en un salón de clases con 25 pupitres?
Solución: El primer estudiante puede elegir entre 25 lugares, el segundo tendrá 24 lugares a escoger, el tercero 23, así sucesivamente; por lo tanto el número de arreglos sin repetición de 25 elementos tomados de 6 en 6 es:
Esto se simboliza por  =
=
Veamos otra aplicación del principio de la multiplicación. Supongamos que tenemos 20 niños de un grupo de Preescolar y 10 sabores de helados disponibles. ¿De cuántas formas diferentes podemos servir un helado a 20 niños?
Al primer niño le podemos servir uno de los 10 sabores, al segundo niño también le podemos servir los 10 sabores, al tercero también, y así sucesivamente. A cada uno de los 20 niños le podemos servir de los 10 sabores, por lo que
Observe que r es el número de veces que se repiten los n elementos.
RESUMEN DE LAS PERMUTACIONES
| DESCRIPCIÓN | FÓRMULA |
| Permutaciones sin repetición de n elementos tomados todos a la vez | |
| Permutaciones circulares de n elementos | |
| Permutaciones sin repetición de n elementos tomados de r en r, donde r £ n | |
| Permutaciones con repetición de n elementos tomados de r en r | |
| Permutaciones de n elementos de los cuales p1son de un tipo, p2 son de otro tipo, ¼ , pk de otro tipo, donde p1 + p2 + ¼ +pk = n. |
COMBINACIONES
son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
NO influye el orden en que se colocan.
Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Ejemplo: Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
Existen dos tipos de combinación: combinación sin repetición y combinación con repetición:
Combinación sin repetición:se definen como las distintas agrupaciones formadas con p elementos distintos, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus elementos).
Combinación con repetición: se definen como las distintas agrupaciones formadas con p elementos que pueden repetirse, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra sólo si difieren en algún elemento, (No influye el orden de colocación de sus elementos).
PROBABILIDAD
La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.
Propiedades de la probabilidad
1. La suma de las probabilidades de un suceso y su contrario vale 1, por tanto la probabilidad del suceso contrario es:

2. Probabilidad del suceso imposible es cero.

3. La probabilidad de la unión de dos sucesos es la suma de sus probabilidades restándole la probabilidad de su intersección.

4. Si un suceso está incluido en otro, su probabilidad es menor o igual a la de éste.

5. Si A1, A2, ..., Ak son incompatibles dos a dos entonces:

6 Si el espacio muestral E es finito y un suceso es S = {x1, x2, ..., xn} entonces:

https://www.vitutor.com/pro/2/a_17.html
https://es.slideshare.net/valentintrs/tcnicas-de-conteo-10538178https://es.wikipedia.org/wiki/Medidas_de_dispersi%C3%B3nhttps://wape23.jimdo.com/unidad-1/1-2-descripci%C3%B3n-de-datos/1-2-1-datos-agrupados-y-no-agrupados/https://es.slideshare.net/pbacelis/datos-agrupados-y-nohttp://shadowsover.blogspot.com.co/2012/07/datos-agrupados-y-no-agrupados_8296.html
https://es.slideshare.net/valentintrs/tcnicas-de-conteo-10538178https://es.wikipedia.org/wiki/Medidas_de_dispersi%C3%B3nhttps://wape23.jimdo.com/unidad-1/1-2-descripci%C3%B3n-de-datos/1-2-1-datos-agrupados-y-no-agrupados/https://es.slideshare.net/pbacelis/datos-agrupados-y-nohttp://shadowsover.blogspot.com.co/2012/07/datos-agrupados-y-no-agrupados_8296.html
 B =
B =  entonces:
entonces: B) = p(A) + p(B)
B) = p(A) + p(B)




No hay comentarios:
Publicar un comentario